The Optimization of the Tendon Routing in a Robotic Gripper
Automatization in the agro- and food industry requires more intricate robotic grippers, which is currently quite a hassle due to how hard grasping (fragile) food products is for machines without intuition. What seems as an easy task for us due to our years of experience, is actually a daunting task for unconscious robots (no matter how clumsy you are, you can put experienced food gripper on your CV, good for when AI takes over our jobs). This is also a good moment to appreciate the marvelous piece of equipment called our hands. The strength of our grip while still having the ability to carefully manipulate objects in such a small form factor is to this date still unmatched. That’s why recreating the intricate mechanism of our hand is such a hot topic inside the research of robotics. The EE graduate Mart Bluiminck recently has proposed a tendon-driven gripper mechanism tailored to the challenges of the agro- and food industry as his Master’s thesis.
A tendon-driven gripper, actuated like our fingers are, to keep a small footprint for the fingers. The gripper proposed by Mart Bluiminck et al. [1] has some really nice features to adapt to object irregularities and to change the joint stiffness during the grasping of an object. It is also able to perform an enveloping grasp (where all phalanges wrap around the object) and a pinching grasp (where only the fingertips touch the object).
The results of the prototype were promising as the previously mentioned characteristics all worked sufficiently and showed room for further research. One of the recommendations was the improvement in the friction experienced by the tendons in the gripper, a notorious challenge of tendon driven mechanisms. That’s where my bachelor’s assignment comes into play. I have researched the optimization of the mechanical design of the gripper to improve the friction in the gripper’s tendon routing.
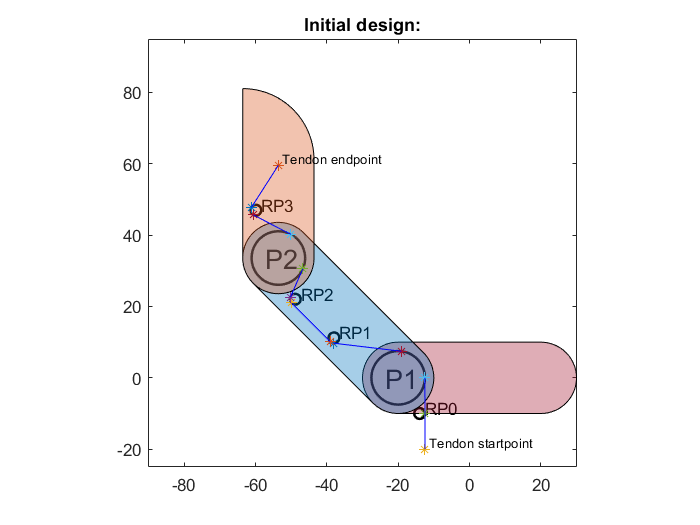
Figure 1: One finger of Mart’s gripper
Problem description
For correct operation, tendon-driven mechanisms require continuous contact between the tendon and the joint pulleys over the full stroke. This is achieved with routing points to ensure the continuous contact with the pulleys.
These routing points introduce new contact points in the tendon drive system which introduces extra friction, which is unwanted because now part of the tension force of the tendons is lost to the friction. This is typically denoted by the force transmission efficiency (FTE), often denoted as ‘eta’, which decreases when a tendon is wrapped around a routing point/pulley. Friction also introduces other unwanted effects, like hysteresis. For my bachelor’s assignment I decided to stick to the improving of the FTE of the system by optimizing the routing point positioning.
Optimization
Cost function
I have used a local minimizer as optimization which, as the name implies, tries to minimize the outcome of a cost function given an initial starting point on the cost function. The expression for the FTE of both the pulley and the routing points is a function of the wrapping angle of the tendon around that object [2]. The wrapping angles are obtained through a lot of geometry by determining the points where the tendon would enter and leave the routing points and pulleys. This results in the cost function that can be seen below.
The eta_tendon is the summation of the FTE of all routing points and pulleys that the tendon will meet in the system. We take the inverse of this eta_tendon to maximise the FTE of all routing points and pulleys.
Soft constraints
I have also added soft constraints to the cost function to ensure continuous contact between the tendon and the pulleys. The ‘D’ variable is positive when the tendon touches the pulley and it is negative when it doesn’t. Both the alpha and gamma are scaling gains which are tuned according to the results of previous optimization runs.
Results
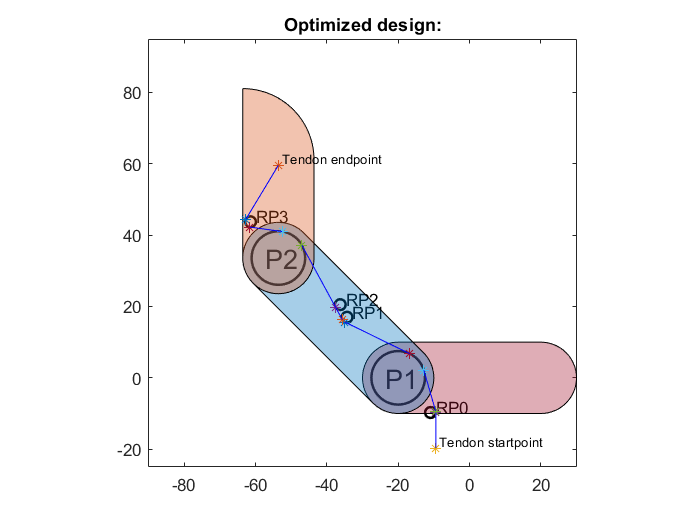
Figure 2: The optimized mechanical design
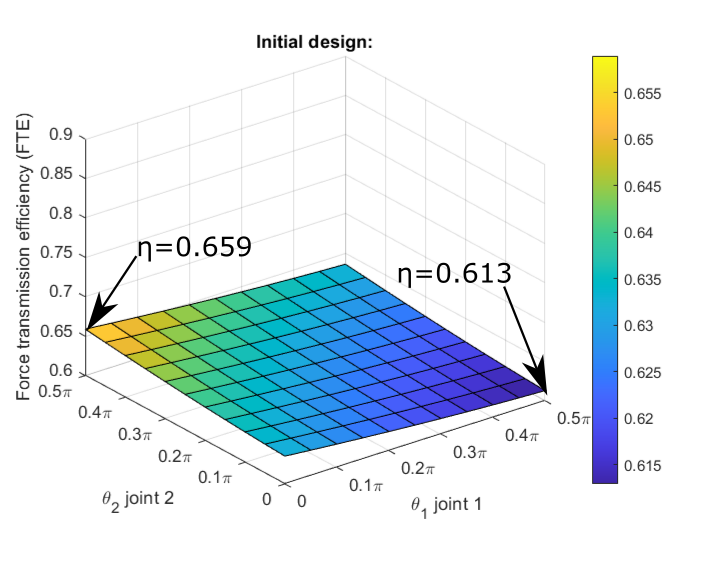
Figure 3: The FTE per joint angle configuration of the initial gripper design. The highest FTE is when the finger is in it’s most bent configuration.
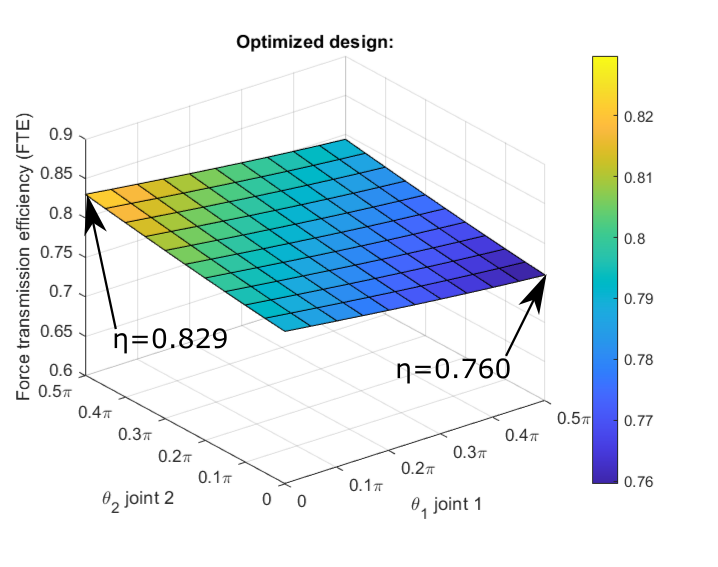
Figure 4: The FTE per joint angle configuration of the optimized gripper design. The highest FTE is when the finger is in it’s most bent configuration.
Conclusion
From the results we can see that the configuration of tendon routing points has changed to improve force transmission efficiency. The results even show that one routing point on the middle phalanx is redundant!
